Особенности влияния дефектов структуры на эффекты корреляции и взаимодействия вихревых возбуждений в неравновесной ВКТ-динамике двумерной XY-модели
Прудников В.В., Прудников П.В., Попов И.С.

Received: May 4, 2020

DOI: 10.31857/S0044451020110139

PDF (18.8M)

Осуществлено численное исследование методом Монте-Карло неравновесного критического поведения двумерной структурно-неупорядоченной XY-модели при ее эволюции из начального высокотемпературного состояния. Выявлены особенности влияния структурного беспорядка на временную зависимость корреляционной длины системы ξ (t) и динамический скейлинг спин-спиновой автокорреляционной функции C_SS(t, t_w). Осуществлен прямой расчет динамического поведения корреляционной длины ξ (t) двумерной структурно-неупорядоченной XY-модели и показано, что для нее, как и для чистой модели, выполняется временная зависимость с логарифмической поправкой 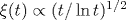, связанная с неравновесной аннигиляцией вихрей и антивихрей в формирующихся вихревых парах. На основе проведенного анализа временных зависимостей корреляционной длины ξ (t) и кумулянта намагниченности g₂(t) показано, что двумерная XY-модель со спиновой концентрацией p = 0.7 находится настолько близко к порогу спиновой перколяции p_c, что влияние притяжения перколяционной неподвижной точки становится определяющим в релаксационных свойствах системы. Однако особенности критической динамики систем со спиновыми концентрациями p = 0.9 и p=0.8 определяются притяжением неподвижной точки чистой системы. Определены температурные и концентрационные зависимости критического индекса Фишера η (p, T) с использованием скейлинговых свойств рассчитанной двухвременной зависимости спин-спиновой автокорреляционной функции C_SS(t, t_w). Осуществлен расчет скейлинговых функций двухвременной зависимости спин-спиновой автокорреляционной функции C_SS(t, t_w) с использованием полученной в результате моделирования динамической зависимости корреляционной длины ξ (t) и определены значения показателей λ _C(p, T) степенного убывания скейлинговых функций в долговременном режиме, находящиеся в хорошем согласии с соотношением λ _C(p, T)= 1 + η (p, T) и доказывающие выполнение динамического скейлинга для неравновесных характеристик структурно-неупорядоченных систем.