Граничные условия, распределение фаз и скрытая симметрия в одномерной локализациии
Суслов И.М.

Поступила в редакцию: 4 Июня 2022

DOI: 10.31857/S0044451022110165

PDF (1797.6K)

Рассматриваются одномерные неупорядоченные системы со случайным потенциалом малой амплитуды и короткодействующими корреляциями для энергий вблизи края зоны идеального кристалла. Получено уравнение эволюции для совместной функции распределения P(ρ ,ψ ) ландауэровского сопротивления ρ и фазовой переменно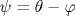й (θ и 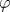- фазы, входящие в трансфер-матрицу) при изменении длины системы L. В пределе больших L уравнение допускает разделение переменных, что обеспечивает существование стационарного распределения P(ψ ), определяющего коэффициенты в уравнении эволюции для P(ρ ). Предельное распределение P(ρ ) при L→ ∞ является логномальным и не зависит от граничных условий. Оно определяется ``внутренним'' распределением фазы ψ , форма которого изучена во всей области энергий, включая запрещенную зону. Приближение случайных фаз справедливо в глубине разрешенной зоны, но сильно нарушается при других энергиях. Фаза ψ оказывается ``плохой'' переменной, а ``правильной'' переменной является ω =-ctgψ /2. Форма стационарного распределения P(ω ) определяется внутренними свойствами системы и не зависит от граничных условий. Изменение граничных условий приводят к масштабному преобразованию ω → sω и трансляциям ω → ω +ω <sub>0</sub> и ψ → ψ +ψ <sub>0</sub>, что определяет ``внешнее'' распределение фаз, входящее в уравнения эволюции. Независимость предельного распределения P(ρ ) от внешнего распределения P(ψ ) позволяет говорить о скрытой симметрии, характер которой выявляется ниже.