
ЖЭТФ, Том 143,
Вып. 1,
стр. 5 (Январь 2013)
(Английский перевод - JETP,
Vol. 116, No 1,
p. 1,
January 2013
доступен on-line на www.springer.com
)
РАСПРОСТРАНЕНИЕ ВОЗБУЖДЕНИЯ В ДЛИННЫХ ОДНОМЕРНЫХ ЦЕПОЧКАХ: ПЕРЕХОД ОТ РЕГУЛЯРНОЙ КВАНТОВОЙ ДИНАМИКИ К СТОХАСТИЧЕСКОЙ
Бендерский В.А., Кац Е.И.
Поступила в редакцию: 17 Мая 2012
DOI: 10.7868/S0044451013010005
Дано аналитическое решение квантовой динамической задачи для одномерной цепочки из 2N+1 узлов (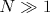 ) с взаимодействием ближайших соседей и примесным узлом в середине, отличающимся от узлов остальной цепочки энергией и константой связи. Начальное возбуждение примеси сопровождается распространением возбуждения по узлам цепочки и появлением эха Лошмидта (частичным восстановлением населенности примесного узла) в циклах возврата, период которых пропорционален N. Эхо состоит из основной (наиболее интенсивной) компоненты, модулированной затухающими осцилляциями. С ростом номера цикла и матричного элемента C взаимодействия примесного узла n=0 с узлами ) с взаимодействием ближайших соседей и примесным узлом в середине, отличающимся от узлов остальной цепочки энергией и константой связи. Начальное возбуждение примеси сопровождается распространением возбуждения по узлам цепочки и появлением эха Лошмидта (частичным восстановлением населенности примесного узла) в циклах возврата, период которых пропорционален N. Эхо состоит из основной (наиболее интенсивной) компоненты, модулированной затухающими осцилляциями. С ростом номера цикла и матричного элемента C взаимодействия примесного узла n=0 с узлами  ( (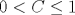 , для остальных соседних узлов матричный элемент равен 1) интенсивность осцилляций увеличивается. Перемешивание компонент эха соседних циклов вызывает переход от регулярной эволюции к стохастической. В области регулярной эволюции волновой пакет распространяется по цепочке с почти постоянной групповой скоростью, охватывая периодически изменяющееся во времени число узлов. В стохастическом режиме возбуждение распределяется по близкому к 2N числу узлов, населенности которых иррегулярно изменяются во времени. Модель качественно объясняет экспериментальные данные по баллистическому распространению колебательной энергии в линейных цепочках из CH2-фрагментов и предсказывает возможность бездиссипативной передачи энергии между реакционными центрами, связанными такими цепочками. , для остальных соседних узлов матричный элемент равен 1) интенсивность осцилляций увеличивается. Перемешивание компонент эха соседних циклов вызывает переход от регулярной эволюции к стохастической. В области регулярной эволюции волновой пакет распространяется по цепочке с почти постоянной групповой скоростью, охватывая периодически изменяющееся во времени число узлов. В стохастическом режиме возбуждение распределяется по близкому к 2N числу узлов, населенности которых иррегулярно изменяются во времени. Модель качественно объясняет экспериментальные данные по баллистическому распространению колебательной энергии в линейных цепочках из CH2-фрагментов и предсказывает возможность бездиссипативной передачи энергии между реакционными центрами, связанными такими цепочками.
|
|