
ZhETF, Vol. 153,
No. 3,
p. 475 (March 2018)
(English translation - JETP,
Vol. 126, No. 3,
p. 397,
March 2018
available online at www.springer.com
)
Устойчивые и неустойчивые вихревые узлы в захваченном бозе-конденсате
Рубан В.П.
Received: November 1, 2017
DOI: 10.7868/S0044451018030136
В гидродинамическом приближении рассмотрена динамика квантового вихревого торического узла 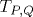 и других подобных узлов в атомном бозе-конденсате, находящемся при нуле температуры в режиме Томаса-Ферми. Конденсат имеет пространственно-неоднородный равновесный профиль плотности ρ (z,r) благодаря действию внешнего осесимметричного потенциала. Предполагается, что z*=0, r*=1 является точкой максимума функции rρ (z,r), причем и других подобных узлов в атомном бозе-конденсате, находящемся при нуле температуры в режиме Томаса-Ферми. Конденсат имеет пространственно-неоднородный равновесный профиль плотности ρ (z,r) благодаря действию внешнего осесимметричного потенциала. Предполагается, что z*=0, r*=1 является точкой максимума функции rρ (z,r), причем 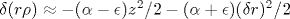 при малых z и δ r. Геометрическая конфигурация узла в цилиндрических координатах определяется комплексной 2π P-периодической функцией при малых z и δ r. Геометрическая конфигурация узла в цилиндрических координатах определяется комплексной 2π P-периодической функцией ![A(\varphi ,t)=Z(\varphi ,t)+i [R(\varphi ,t)-1]](/img/latex/Ax28x5cvarphix20x2ctx29x3dZx28x5cvarphix20x2ctx29x2bix20x5bRx28x5cvarphix20x2ctx29x2d1x5d.png) . В случае . В случае  система описывается относительно простыми приближенными уравнениями для перемасштабированных функций система описывается относительно простыми приближенными уравнениями для перемасштабированных функций 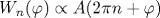 в количестве P штук: в количестве P штук: 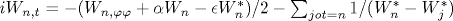 . При ε =0 численно найдены для P=3 примеры устойчивых решений вида . При ε =0 численно найдены для P=3 примеры устойчивых решений вида 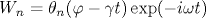 с нетривиальной топологией. Кроме того, промоделирована динамика различных нестационарных узлов с P=3, причем в ряде случаев замечена тенденция к образованию особенности за конечное время. Для P=2 при малых ε
ot =0 исследованы вращающиеся вокруг оси z конфигурации вида с нетривиальной топологией. Кроме того, промоделирована динамика различных нестационарных узлов с P=3, причем в ряде случаев замечена тенденция к образованию особенности за конечное время. Для P=2 при малых ε
ot =0 исследованы вращающиеся вокруг оси z конфигурации вида 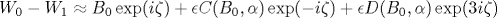 , где B0, k0=Q/2, Ω 0=(k02-α )/2-2/B02. В пространстве параметров (α , B0) обнаружены широкие области устойчивости таких решений. При этом в неустойчивых зонах возможен возврат вихревого узла к слабо возбужденному состоянию. , где B0, k0=Q/2, Ω 0=(k02-α )/2-2/B02. В пространстве параметров (α , B0) обнаружены широкие области устойчивости таких решений. При этом в неустойчивых зонах возможен возврат вихревого узла к слабо возбужденному состоянию.
|
|