Распределение кондактансов вблизи перехода Андерсона
Суслов И.М.

Received: July 12, 2016

DOI: 10.7868/S0044451017050121

PDF (911.8K)

С помощью модификации метода Шапиро вводится двухпараметрическое семейство распределений кондактанса W(g), определяемое простыми дифференциальными уравнениями, которое находится во взаимно-однозначном соответствии с распределениями кондактанса квазиодномерных систем размера 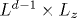, характеризуемых параметрами L/ξ и L_z/L (ξ - корреляционный радиус, d - размерность пространства). Это семейство содержит гауссовские и логнормальные распределения, характерные для металлической и локализованной фаз. При определенном выборе параметров воспроизводятся результаты для кумулянтных средних в пространстве размерности d=2+ε , полученные с помощью нелинейной сигма-модели. Универсальным свойством распределения является существование двух асимптотик - логнормальной для малых g и экспоненциальной при больших g: в металлической фазе они относятся к далеким хвостам, в критической области - определяют практически все распределение, в локализованной фазе первая асимптотика вытесняет вторую. Сингулярность при g=1, обнаруженная в численных экспериментах, вполне допустима в рамках использованной в них вычислительной схемы, но связана с дефектным определением проводимости. За исключением этой сингулярности, критическое распределение для d=3 хорошо описывается настоящей теорией. Однопараметрический скейлинг для распределения в целом имеет место при условии, что два независимых параметра, характеризующих это распределение, являются функциями только от L/ξ .