НЕЛИНЕЙНОЕ УРАВНЕНИЕ ВЫСОКОГО ПОРЯДКА ДЛЯ ОГИБАЮЩЕЙ ГРАВИТАЦИОННЫХ ВОЛН НА ВОДЕ КОНЕЧНОЙ ГЛУБИНЫ
Слюняев А.В.

Received: April 8, 2005

PACS: 05.45.-a, 47.20.-k, 47.35.+i, 92.10.Hm

DJVU (156.5K)

PDF (336.6K)

Получено уравнение для огибающей волн на поверхности воды конечной глубины, включающее члены трех порядков малости. Используются предположения о малости крутизны волн, узости спектра и малости глубины по сравнению с длиной модуляции. В случае достаточно глубокой воды выведено обобщенное уравнение Диста. В пределе мелкой воды в уравнении исчезает одно из слагаемых нелинейной дисперсии. Этот предел сопоставлен с уравнением для огибающей волн, описываемых уравнением Кортевега - де Вриза. Исследован пограничный случай вырождения нелинейности в классическом нелинейном уравнении Шредингера для волн на воде (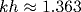). Показано, что для интенсивных волн порог модуляционной неустойчивости сдвигается в область более мелкой воды (длинных волн).