
ZhETF, Vol. 121,
No. 4,
p. 971 (April 2002)
(English translation - JETP,
Vol. 94, No. 4,
p. 834,
April 2002
available online at www.springer.com
)
СТАТИСТИЧЕСКИЙ ПРЕДЕЛ В РЕШЕНИИ НЕЛИНЕЙНОГО УРАВНЕНИЯ ШРЕДИНГЕРА ПРИ ДЕТЕРМИНИРОВАННЫХ НАЧАЛЬНЫХ УСЛОВИЯХ
Мазур Н.Г., Геогджаев В.В., Гуревич А.В., Зыбин К.П.
Received: July 25, 2001
PACS: 05.10.-a, 05.45.Yv
Исследуется квазиклассический предел для нелинейного уравнения Шредингера в случае дефокусирующей среды при осциллирующих непериодических заданных на всей оси x начальных условиях. Сформулирована система интегральных законов сохранения в форме бесконечного числа усредненных по пространству плотностей, которые рассчитываются явно по начальным условиям. Исследована прямая задача рассеяния и показано, что фаза рассеяния является равномерно распределенной случайной величиной. Эволюция такой системы приводит к развитию нелинейных колебаний, приобретающих на больших временах статистический характер. Асимптотическое решение построено методом модифицированной обратной задачи рассеяния, основанным на конструкции максимизатора N-солитонного решения в континуальном пределе при 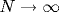 . С помощью максимизатора найден бесконечный набор cохраняющихся усредненных плотностей в статистическом состоянии. Это позволило связать начальное состояние с установившимся при . С помощью максимизатора найден бесконечный набор cохраняющихся усредненных плотностей в статистическом состоянии. Это позволило связать начальное состояние с установившимся при 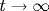 предельным статистическим и тем самым однозначно определить спектр уровней в статистическом состоянии. предельным статистическим и тем самым однозначно определить спектр уровней в статистическом состоянии.
|
|