
ЖЭТФ, Том 127,
Вып. 6,
стр. 1350 (Июнь 2005)
(Английский перевод - JETP,
Vol. 100, No 6,
p. 1188,
June 2005
доступен on-line на www.springer.com
)
РАСХОДЯЩИЕСЯ РЯДЫ ТЕОРИИ ВОЗМУЩЕНИЙ
Суслов И.М.
Поступила в редакцию: 20 Января 2005
PACS: 03.65.-w, 11.10.Hi, 71.23.An
Многие ряды теории возмущений расходятся факториально. Их поведение в высоких порядках может быть найдено методом Липатова и определяется перевальными конфигурациями - инстантонами - соответствующих функциональных интегралов. Знание асимптотики Липатова и нескольких первых членов ряда, полученных путем прямых диаграммных вычислений, дает информацию обо всех членах ряда, суммирование которого позволяет в некотором приближении решить многие проблемы сильной связи. Этот подход демонстрируется на примере восстановления функций Гелл-Манна - Лоу теории 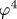 , КЭД и КХД при произвольных константах связи. Представлен обзор математической теории расходящихся рядов и показано, в каком смысле понимаются ряды теории возмущений. Дан наглядный вывод асимптотики Липатова для основных задач теоретической физики. Предложено решение проблемы ренормалонных вкладов, затормозившей развитие всего направления в конце 1970-х годов. Изложены методы практического суммирования рядов теории возмущений для константы связи порядка 1 и в пределе сильной связи. Дана интерпретация борелевского интеграла для рядов, «не суммируемых по Борелю». Обсуждается вычисление высших поправок к асимптотике Липатова. , КЭД и КХД при произвольных константах связи. Представлен обзор математической теории расходящихся рядов и показано, в каком смысле понимаются ряды теории возмущений. Дан наглядный вывод асимптотики Липатова для основных задач теоретической физики. Предложено решение проблемы ренормалонных вкладов, затормозившей развитие всего направления в конце 1970-х годов. Изложены методы практического суммирования рядов теории возмущений для константы связи порядка 1 и в пределе сильной связи. Дана интерпретация борелевского интеграла для рядов, «не суммируемых по Борелю». Обсуждается вычисление высших поправок к асимптотике Липатова.
|
|