Журнал Экспериментальной и Теоретической Физики

НАЧАЛО | ПОИСК | ДЛЯ АВТОРОВ | ПОМОЩЬ

Общая информация о журнале

Проверить статус статьи

ЖЭТФ, Том 148, Вып. 3, стр. 514 (Сентябрь 2015)
(Английский перевод - JETP, Vol. 121, No 3, p. 446, September 2015 доступен on-line на www.springer.com )

СПИН-СПИНОВАЯ КОРРЕЛЯЦИОННАЯ ДЛИНА В ДВУМЕРНОМ ФРУСТРИРОВАННОМ МАГНЕТИКЕ И ЕЕ СВЯЗЬ С ДОПИРОВАНИЕМ
Михеенков А.В., Валиулин В.Э., Шварцберг А.В., Барабанов А.Ф.

Поступила в редакцию: 26 Марта 2015

DOI: 10.7868/S0044451015090096

DJVU (281.1K) PDF (913.7K)

В сферически-симметричном самосогласованном подходе для двухвременных запаздывающих спин-спиновых функций Грина рассматривается J₁-J₂-модель Гейзенберга для спина S=1/2 на двумерной квадратной решетке. Получен спектр спиновых возбуждений, ω( q), и спиновые щели в симметричных точках для всего J₁-J₂-круга, т. е. для любого 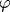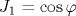$\varphi$ , $J_1=\cos\varphi$ , $J_2=\sin\varphi$ . Во всем диапазоне параметров вычислен структурный фактор c_q и корреляционная длина ξ при конечной температуре. 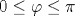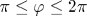Продемонстрировано коренное различие поведения системы в верхней, фрустрированной ( $0\leq\varphi\leq\pi$ ), и нижней, нефрустрированной ( $\pi\leq\varphi\leq2\pi$ ), областях круга. В последней содержится единственный на фазовой диаграмме переход первого рода. Для слабофрустрированного антиферромагнетика (J₁₂

Сообщить о технических проблемах