ПРОВОДИМОСТЬ КОНЕЧНЫХ СИСТЕМ И СКЕЙЛИНГ В ТЕОРИИ ЛОКАЛИЗАЦИИ
Суслов И.М.

Поступила в редакцию: 17 Февраля 2012

DJVU (407.2K)

PDF (715K)

Полная проводимость (кондактанс) конечной системы играет центральную роль в скейлинговой теории локализации [1]. Обычно она определяется формулами Ландауэра, в которых остаются непроясненными вопросы: а) об исключении контактного сопротивления в многоканальном случае; б) о соответствии ландауэровской проводимости внутренним свойствам системы; в) о связи с коэффициентом диффузии D(ω,q) бесконечной системы. Ответ на эти вопросы получен ниже в рамках двух подходов: (1) самосогласованной теории локализации Вольхардта - Вольфле и (2) квантовомеханического анализа, основанного на модели оболочек. Оба подхода приводят к одинаковому определению проводимости конечной системы, тесно связанному с определением Таулеса. В рамках самосогласованной теории получены соотношения конечно-размерного скейлинга и вычислены функции Гелл-Манна - Лоу β(g) для размерностей пространства d=1, 2, 3. В отличие от ранних попыток такого рода [24], металлическая и локализованная фазы рассматриваются единым образом, так что кондактанс конечной системы не имеет сингулярности в критической точке. В двумерном случае разложение β(g) по 1/g согласуется с результатами σ-моделей в двухпетлевом приближении и зависит от ренормировочной схемы в высших петлях; использование же размерной регуляризации для перехода к d=2+ε, по-видимому, несовместимо с физической сутью проблемы. Проведено сопоставление с результатами численного моделирования и физическим экспериментом. Обсуждаются условия наблюдения локализационного закона 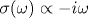для проводимости и ситуация в высших размерностях.