
ZhETF, Vol. 165,
No. 2,
p. 233 (February 2024)
(English translation - JETP,
Vol. 138, No. 2,
February 2024
available online at www.springer.com
)
Распределение фаз в одномерной локализации и фазовые переходы в одномодовых волноводах
Суслов И.М.
Received: May 31, 2023
DOI: 10.31857/S0044451024020093
Локализация электронов в одномерных неупорядоченных системах обычно описывается в рамках приближения случайных фаз, когда распределения фаз 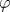 и θ , входящих в трансфер-матрицу, считаются однородными. В общем случае приближение случайных фаз нарушается, и уравнения эволюции (при изменении длины системы L) содержат три независимые переменные - ландауэровское сопротивление ρ и комбинированные фазы и θ , входящих в трансфер-матрицу, считаются однородными. В общем случае приближение случайных фаз нарушается, и уравнения эволюции (при изменении длины системы L) содержат три независимые переменные - ландауэровское сопротивление ρ и комбинированные фазы 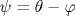 и и 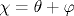 . Фаза χ не влияет на эволюцию ρ и не рассматривалась в предыдущих работах. Распределение фазы ψ при изменении энергии электрона . Фаза χ не влияет на эволюцию ρ и не рассматривалась в предыдущих работах. Распределение фазы ψ при изменении энергии электрона 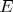 испытывает своеобразный фазовый переход в точке испытывает своеобразный фазовый переход в точке 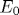 , состоящий в появлении у ψ мнимой части. Распределение сопротивлений P(ρ ) не имеет сингулярности в точке , состоящий в появлении у ψ мнимой части. Распределение сопротивлений P(ρ ) не имеет сингулярности в точке 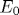 и переход выглядит ненаблюдаемым в электронных системах. Однако теория одномерной локализации непосредственно применима к распространению волн в одномодовых волноводах. Оптические методы более эффективны и обеспечивают возможность измерения фаз ψ и χ . С одной стороны, это делает наблюдаемым фазовый переход в распределении P(ψ ), который можно рассматривать как «след» от порога подвижности, сохраняющийся в одномерных системах. С другой стороны, фаза χ становится наблюдаемой: это делает актуальным вывод уравнения для ее эволюции, который производится ниже. Релаксация распределения P(χ ) к предельному распределению P∞ (χ ) при L→ ∞ описывается двумя экспонентами, показатели которых испытывают разрыв второй производной при изменении энергии и переход выглядит ненаблюдаемым в электронных системах. Однако теория одномерной локализации непосредственно применима к распространению волн в одномодовых волноводах. Оптические методы более эффективны и обеспечивают возможность измерения фаз ψ и χ . С одной стороны, это делает наблюдаемым фазовый переход в распределении P(ψ ), который можно рассматривать как «след» от порога подвижности, сохраняющийся в одномерных системах. С другой стороны, фаза χ становится наблюдаемой: это делает актуальным вывод уравнения для ее эволюции, который производится ниже. Релаксация распределения P(χ ) к предельному распределению P∞ (χ ) при L→ ∞ описывается двумя экспонентами, показатели которых испытывают разрыв второй производной при изменении энергии 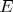 . .
|
|