Электрон-фононная связь в теории Элиашберга-Макмиллана за пределами адиабатического приближения
Садовский М.В.

Received: August 14, 2018

DOI: 10.1134/S0044451019030155

PDF (262.5K)

Теория сверхпроводимости Элиашберга-Макмиллана основана на применимости адиабатического приближения. Параметр малости теории возмущений имеет при этом вид 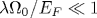, где λ - безразмерная константа электрон-фононного взаимодействия, Ω ₀ - характерная частота фононов, а E_F - энергия Ферми электронов. В данной работе предпринята попытка описания электрон-фононного взаимодействия в рамках подхода Элиашберга-Макмиллана в ситуации, когда характерная частота фононов Ω ₀ становится достаточно большой (сравнимой или превышающей энергию Ферми E_F). Рассматривается общее определение спаривательной электрон-фононной константы связи λ , с учетом конечности частоты фононов. Получено простое выражение для обобщенной константы связи , определяющей перенормировку массы, с учетом конечной ширины зоны проводимости, описывающее плавный переход от адиабатического режима в область неадиабатичности. В условиях сильной неадиабатичности, когда , в теории возникает новый параметр малости (D - полуширина электронной зоны), а поправки к электронному спектру становятся несущественными. В то же время, температура сверхпроводящего перехода T_c и в антиадиабатическом пределе определяется спаривательной константой связи Элиашберга-Макмиллана λ , а предэкспоненциальный множитель в формуле для T_c, сохраняющей типичный вид для приближения слабой связи, определяется шириной зоны (энергией Ферми). Для случая взаимодействия с одним оптическим фононом получена единая формула для T_c, справедливая как в адиабатическом, так и в антиадиабатическом режимах. Полученные результаты обсуждаются в контексте проблемы высокотемпературной сверхпроводимости в системе FeSe/STO.