
ZhETF, Vol. 150,
No. 2,
p. 372 (August 2016)
(English translation - JETP,
Vol. 123, No. 2,
p. 322,
August 2016
available online at www.springer.com
)
Электрон в поле изгибных колебаний мембраны: квантовое время, магнитоосцилляции и разрушение когерентности
Горный И.В., Дмитриев А.П., Мирлин А.Д., Протопопов И.В.
Received: January 13, 2016
DOI: 10.7868/S0044451016080186
Изучено движение электрона в мембране под влиянием равновесных изгибных колебаний, коррелятор которых убывает с расстоянием по закону r-2η . Подробно рассмотрен случай η <1/2, когда даже при сколь угодно слабом взаимодействии теория возмущений неприменима. Показано, что в этом случае обратное квантовое время 1/τ q пропорционально g1/(1-η )T(2-η )/(2-2η ), где g - константа электрон-фононного взаимодействия, а T - температура. Развитый метод приложен к вычислению плотности состояний электрона в перпендикулярном к мембране магнитном поле. Показано, в частности, что в режиме 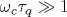 уровни Ландау имеют гауссову форму с шириной, зависящей от магнитного поля по закону Bη . Кроме того, вычислено время сбоя фазы волновой функции электрона уровни Ландау имеют гауссову форму с шириной, зависящей от магнитного поля по закону Bη . Кроме того, вычислено время сбоя фазы волновой функции электрона 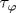 за счет его взаимодействия с изгибными фононами в случае η <1/2. Показано, что имеется несколько температурных интервалов, в которых величина за счет его взаимодействия с изгибными фононами в случае η <1/2. Показано, что имеется несколько температурных интервалов, в которых величина 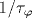 выражается различными степенными функциями от константы электрон-фононного взаимодействия, температуры и энергии электрона. выражается различными степенными функциями от константы электрон-фононного взаимодействия, температуры и энергии электрона.
|
|