ZhETF, Vol. 146,
No. 6,
p. 1272 (December 2014)
(English translation - JETP,
Vol. 119, No. 6,
p. 1115,
December 2014
available online at www.springer.com
)
ИНТЕРПРЕТАЦИЯ ЧИСЛЕННЫХ ДАННЫХ ДЛЯ ПЕРЕХОДА АНДЕРСОНА В ВЫСОКОЙ РАЗМЕРНОСТИ
Суслов И.М.
Received: May 28, 2014
DOI: 10.7868/S004445101412013X
Существование верхней критической размерности dc2=4 для перехода Андерсона является строгим следствием теоремы Боголюбова о перенормируемости теории φ4. Для размерностей 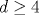 однопараметрический скейлинг не имеет места и все существующие численные данные должны быть переинтерпретированы. Они сводятся к результатам для d=4, 5, полученным из скейлинга в квазиодномерных системах, и результатам для d=4, 5, 6 из скейлинга для статистики уровней. Все эти данные оказываются совместимыми с теоретическими скейлинговыми зависимостями, полученными из самосогласованной теории Вольхардта - Вольфле. Дано критическое обсуждение широко распространенной точки зрения о том, что dc2=∞. Статья для специального выпуска ЖЭТФ, посвященного 75-летию А. Ф. Андреева}
|
|
Golden Pages
DJVU (142.5K)
PDF (320.4K)