ENERGY SPECTRUM OF THE ENSEMBLE OF WEAKLY NONLINEAR GRAVITY-CAPILLARY WAVES ON A FLUID SURFACE
Tobisch E.

Received: March 27, 2014

DOI: 10.7868/S0044451014080173

DJVU (85.3K)

PDF (219.4K)

We consider nonlinear gravity-capillary waves with the nonlinearity parameter 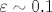-0.25. For this nonlinearity, time scale separation does not occur and the kinetic wave equation does not hold. An energy cascade in this case is built at the dynamic time scale (D-cascade) and is computed by the increment chain equation method first introduced in [15]. We for the first time compute an analytic expression for the energy spectrum of nonlinear gravity-capillary waves as an explicit function of the ratio of surface tension to the gravity acceleration. We show that its two limits - pure capillary and pure gravity waves on a fluid surface - coincide with the previously obtained results. We also discuss relations of the D-cascade model with a few known models used in the theory of nonlinear waves such as Zakharov's equation, resonance of modes with nonlinear Stokes-corrected frequencies, and the Benjamin-Feir index. These connections are crucial in understanding and forecasting specifics of the energy transport in a variety of multicomponent wave dynamics, from oceanography to optics, from plasma physics to acoustics.