
ZhETF, Vol. 144,
No. 5,
p. 972 (November 2013)
(English translation - JETP,
Vol. 117, No. 5,
p. 846,
November 2013
available online at www.springer.com
)
КРОССИНГ-РЕЗОНАНС ВОЛНОВЫХ ПОЛЕЙ В СРЕДЕ С НЕОДНОРОДНЫМ ПАРАМЕТРОМ СВЯЗИ
Игнатченко В.А., Полухин Д.С.
Received: June 4, 2013
DOI: 10.7868/S0044451013110096
Исследованы динамические восприимчивости (функции Грина) системы двух связанных волновых полей различной физической природы в среде с произвольным соотношением между средним значением  и среднеквадратичной флуктуацией и среднеквадратичной флуктуацией 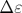 параметра связи. Самосогласованное приближение, учитывающее все диаграммы с непересекающимися линиями корреляций, развито для случая, когда исходная функция Грина однородной среды описывает систему связанных волновых полей. Исследование проведено на примере спиновых и упругих волн. Получены выражения для диагональных элементов Gmm и Guu матричной функции Грина, описывающих спиновые и упругие волны при магнитном и упругом возбуждении, и недиагональных элементов Gmu и Gum, описывающих эти волны при перекрестном возбуждении. Численно исследовано изменение формы этих элементов для случая одномерных неоднородностей с ростом параметра связи. Самосогласованное приближение, учитывающее все диаграммы с непересекающимися линиями корреляций, развито для случая, когда исходная функция Грина однородной среды описывает систему связанных волновых полей. Исследование проведено на примере спиновых и упругих волн. Получены выражения для диагональных элементов Gmm и Guu матричной функции Грина, описывающих спиновые и упругие волны при магнитном и упругом возбуждении, и недиагональных элементов Gmu и Gum, описывающих эти волны при перекрестном возбуждении. Численно исследовано изменение формы этих элементов для случая одномерных неоднородностей с ростом 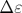 и уменьшением и уменьшением  при условии сохранения суммы квадратов этих величин: уширение и последующее слияние двух пиков на частотных зависимостях мнимых частей Gmm и Guu в один широкий пик; возникновение и формирование тонкой структуры в форме узкого резонанса на вершине функции Грина одного волнового поля и узкого антирезонанса на вершине функции Грина другого поля; рост ширины пиков тонкой структуры и последующее исчезновение их с ростом корреляционного волнового числа неоднородностей параметра связи; уменьшение амплитуд недиагональных элементов до нуля при при условии сохранения суммы квадратов этих величин: уширение и последующее слияние двух пиков на частотных зависимостях мнимых частей Gmm и Guu в один широкий пик; возникновение и формирование тонкой структуры в форме узкого резонанса на вершине функции Грина одного волнового поля и узкого антирезонанса на вершине функции Грина другого поля; рост ширины пиков тонкой структуры и последующее исчезновение их с ростом корреляционного волнового числа неоднородностей параметра связи; уменьшение амплитуд недиагональных элементов до нуля при 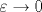 . .
|
|