Journal of Experimental and Theoretical Physics
HOME | SEARCH | AUTHORS | HELP      
Journal Issues
Golden Pages
About This journal
Aims and Scope
Editorial Board
Manuscript Submission
Guidelines for Authors
Manuscript Status
Contacts

ZhETF, Vol. 141, No. 1, p. 47 (January 2012)
(English translation - JETP, Vol. 114, No. 1, p. 39, January 2012 available online at www.springer.com )

FERMIONIC SCREENINGS AND LINE BUNDLE TWISTED CHIRAL DE RHAM COMPLEX ON CY MANIFOLDS
Parkhomenko S.E.

Received: June 1, 2011

DJVU (106.6K) PDF (240K)

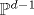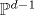We present a generalization of Borisov's construction of the chiral de Rham complex in the case of the line-bundle-twisted chiral de Rham complex on a Calabi-Yau hypersurface in a projective space. We generalize the differential associated with a polytope Δ of the projective space \mathbb{P}^{d- 1} by allowing nonzero modes for the screening currents forming this differential. It is shown that the numbers of screening current modes define the support function of the toric divisor of a line bundle on \mathbb{P}^{d-1} that twists the chiral de Rham complex on the Calabi-Yau hypersurface.

 
Report problems