
ZhETF, Vol. 138,
No. 5,
p. 881 (November 2010)
(English translation - JETP,
Vol. 111, No. 5,
p. 776,
November 2010
available online at www.springer.com
)
ВНУТРЕННИЕ ВОЛНЫ В СЖИМАЕМОЙ ДВУХСЛОЙНОЙ МОДЕЛИ АТМОСФЕРЫ: ГАМИЛЬТОНОВО ОПИСАНИЕ
Рубан В.П.
Received: April 15, 2010
Рассмотрены медленные в сравнении со скоростью звука движения идеальной сжимаемой жидкости (газа) в поле тяжести при наличии двух изэнтропических слоев с небольшой разницей удельной энтропии между ними. В предположении потенциальности течения в каждом из слоев (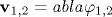 ) и в пренебрежении звуковыми степенями свободы ( ) и в пренебрежении звуковыми степенями свободы (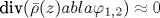 , где , где 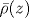 - средняя равновесная плотность) выведены уравнения движения границы раздела в терминах формы самой поверхности z=η(x,y,t) и разности граничных значений двух потенциалов поля скорости: ψ(x,y,t)=ψ1- ψ2. Доказана гамильтонова структура полученных уравнений, задаваемая лагранжианом вида \cL=\int \barρ(η)ηtψ dx dy -\cH{η,ψ}. Рассматриваемая система является простейшей теоретической моделью для изучения внутренних волн в резко стратифицированной атмосфере, в которой существенно учитывается уменьшение равновесной плотности газа за счет его сжимаемости при увеличении высоты. Для плоских течений сделано обобщение на случай, когда в каждом из слоев имеется своя постоянная потенциальная завихренность. Исследована система с модельной зависимостью - средняя равновесная плотность) выведены уравнения движения границы раздела в терминах формы самой поверхности z=η(x,y,t) и разности граничных значений двух потенциалов поля скорости: ψ(x,y,t)=ψ1- ψ2. Доказана гамильтонова структура полученных уравнений, задаваемая лагранжианом вида \cL=\int \barρ(η)ηtψ dx dy -\cH{η,ψ}. Рассматриваемая система является простейшей теоретической моделью для изучения внутренних волн в резко стратифицированной атмосфере, в которой существенно учитывается уменьшение равновесной плотности газа за счет его сжимаемости при увеличении высоты. Для плоских течений сделано обобщение на случай, когда в каждом из слоев имеется своя постоянная потенциальная завихренность. Исследована система с модельной зависимостью 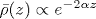 , при которой гамильтониан \cH{η,ψ} удается представить в явном виде. Рассмотрен длинноволновый динамический режим с учетом дисперсионных поправок и выведено приближенное нелинейное уравнение вида , при которой гамильтониан \cH{η,ψ} удается представить в явном виде. Рассмотрен длинноволновый динамический режим с учетом дисперсионных поправок и выведено приближенное нелинейное уравнение вида ![u_t+auu_x-b[-\hat\partial_x^2+\alpha^2]^{1/2}u_x=0](/img/latex/ux5ftx2bauux5fx78x2dbx5bx2dx5chatx5cpartialx5fx78x5e2x2bx5calphax5e2x5dx5ex7b1x2f2x7dux5fx78x3d0.png) (уравнение Смита) для медленной эволюции бегущей волны. (уравнение Смита) для медленной эволюции бегущей волны.
|
|