Journal of Experimental and Theoretical Physics

HOME | SEARCH | AUTHORS | HELP

Journal Issues

Manuscript Submission

Guidelines for Authors

Manuscript Status

Contacts

ZhETF, Vol. 137, No. 3, p. 530 (March 2010)
(English translation - JETP, Vol. 110, No. 3, p. 469, March 2010 available online at www.springer.com )

МОДЕЛИРОВАНИЕ СОПРОТИВЛЕНИЯ И ЕМКОСТИ СЕЛЕНИДА МЫШЬЯКА ФРАКТАЛЬНЫМ МЕТОДОМ
Балханов В.К., Башкуев Ю.Б.

Received: March 5, 2009

DJVU (66.1K) PDF (238K)

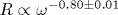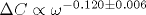Немногим более 40 лет назад были измерены [1] температурные зависимости сопротивления R и емкости C на переменном токе для селенида мышьяка. Из результатов этих измерений следуют частотные характеристики: $R\propto\omega^{-0.80\pm 0.01}$ и $\Delta C\propto\omega^{-0.120\pm0.006}$ (ω - круговая частота, Δ C отсчитывается от не зависящего от температуры значения C₀). 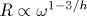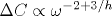Согласно методам фрактальной геометрии, $R\propto\omega^{1-3/h}$ и $\Delta C\propto\omega^{-2+3/h}$ , где h - размерность блуждания электрического тока в селениде мышьяка. 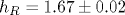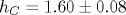Из сравнения экспериментальных и теоретических результатов следует, что размерность блуждания, вычисленная по частотной характеристике сопротивления, равна $h_R=1.67\pm0.02$ , а по частотной характеристике емкости - $h_C=1.60\pm 0.08$ . В пределах ошибок измерения оба значения, h_R и h_C, согласуются друг с другом. Фрактальная размерность распределения проводящих участков D=1/h=0.6. Поскольку D<1, проводящие участки пространственно разделены и образуют канторовское множество.

Report problems