СТАТИСТИЧЕСКАЯ МОДЕЛЬ МЕРЦАЮЩЕЙ ФЛУОРЕСЦЕНЦИИ
Учайкин В.В., Сибатов Р.Т.

Received: March 21, 2009

PACS: 78.67.Bf

DJVU (156.6K)

PDF (425.1K)

Мерцание одиночных молекул и нанокристаллов рассматривается как бинарный случайный процесс восстановления с двумя состояниями: on (излучающее) и off (не излучающее). Длительности пребывания в on- или off-состояниях могут быть распределены по степенному или по экспоненциальному законам. С помощью дробного обобщения экспоненциальной функции дано единое описание процесса мерцания для обоих типов распределений. На основе бинарной модели получено уравнение для плотности распределения p(t_on|t) суммарного времени свечения за время наблюдения t. Для случая степенного мерцания оно содержит производные дробных порядков α и β, совпадающих с показателями степенных on-, off-распределений. В пределе α=β=1 распределения переходят в экспоненциальные, а дробно-дифференциальное уравнение - в уравнение с производными целых порядков. Решения этих уравнений выражены через дробно-устойчивые распределения. Пуассоновское преобразование плотности p(t_on|t) приводит к распределению числа испущенных фотонов и определяет статистику счета. Показано, что временная зависимость параметра Манделя в асимптотике больших времен является степенной: 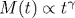. Определена зависимость γ(α,β) на плоскости (α,β). При анализе относительных флуктуаций времени свечения было выяснено, что они убывают только в случаях α=β=1 и α<β. При всех остальных соотношениях α и β относительные флуктуации в асимптотике возрастают по степенному закону либо стремятся к постоянной величине. Аналитические расчеты хорошо согласуются с результатами моделирования методом Монте-Карло.