
ZhETF, Vol. 130,
No. 5,
p. 931 (November 2006)
(English translation - JETP,
Vol. 103, No. 5,
p. 808,
November 2006
available online at www.springer.com
)
КРИТИЧЕСКИЕ СВОЙСТВА ВЫСОКОСПИНОВЫХ МОДЕЛЕЙ ИЗИНГА НА АНИЗОТРОПНОЙ РЕШЕТКЕ
Юрищев М.А.
Received: April 6, 2006
PACS: 05.50.+q, 05.70.Jk, 64.60.Fr, 75.10.Hk
Рассчитаны координаты критических точек S-спиновых (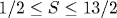 ) моделей Изинга на двумерной прямоугольной решетке с константами взаимодействия J и ) моделей Изинга на двумерной прямоугольной решетке с константами взаимодействия J и 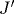 . Вычисления при различных S и . Вычисления при различных S и 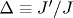 проведены двумя независимыми способами: в рамках феноменологической ренормгруппы и с использованием (приближенной) дуальной симметрии. Расчеты (численные и, дополнительно, в приближении среднего поля) показывают, что при проведены двумя независимыми способами: в рамках феноменологической ренормгруппы и с использованием (приближенной) дуальной симметрии. Расчеты (численные и, дополнительно, в приближении среднего поля) показывают, что при 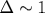 (слабоанизотропная решетка) критическое взаимодействие Kc(S)(Δ)=Kc(S)(1) [1+a(1-Δ)], причем a=(d-1)/d не зависит от S (d - размерность пространства). В критических точках найдены свободная и внутренняя энергии. Обнаружено существование экстремума на зависимости критической внутренней энергии при (слабоанизотропная решетка) критическое взаимодействие Kc(S)(Δ)=Kc(S)(1) [1+a(1-Δ)], причем a=(d-1)/d не зависит от S (d - размерность пространства). В критических точках найдены свободная и внутренняя энергии. Обнаружено существование экстремума на зависимости критической внутренней энергии при 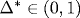 . Предложено использовать параметр Δ* в качестве критерия квазиодномерности - порога, до которого простирается квазиизотропная ( . Предложено использовать параметр Δ* в качестве критерия квазиодномерности - порога, до которого простирается квазиизотропная (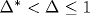 ) область и ниже которого начинается квазиодномерный (Δ<Δ*) режим поведения системы. Оценены величины критических конечно-размерных скейлинговых амплитуд As и Ae обратных корреляционных длин корреляционных функций соответственно спин-спин и энергия-энергия. Расчеты свидетельствуют, что в пределах погрешностей использованных приближений амплитуды As и Ae не зависят от величины спина S, а их отношение Ae/As, кроме того, не зависит от степени анизотропии Δ решетки. Это подтверждает гипотезу универсальности. ) область и ниже которого начинается квазиодномерный (Δ<Δ*) режим поведения системы. Оценены величины критических конечно-размерных скейлинговых амплитуд As и Ae обратных корреляционных длин корреляционных функций соответственно спин-спин и энергия-энергия. Расчеты свидетельствуют, что в пределах погрешностей использованных приближений амплитуды As и Ae не зависят от величины спина S, а их отношение Ae/As, кроме того, не зависит от степени анизотропии Δ решетки. Это подтверждает гипотезу универсальности.
|
|