
ZhETF, Vol. 129,
No. 4,
p. 664 (April 2006)
(English translation - JETP,
Vol. 102, No. 4,
p. 582,
April 2006
available online at www.springer.com
)
THE SYMMETRY RELATING THE PROCESSES IN 2- AND 4-DIMENSIONAL SPACE-TIMES, AND THE VALUE \alpha_0 = 1/4\pi OF THE BARE FINE STRUCTURE CONSTANT
Ritus V.I.
Received: April 22, 2005
PACS: 11.10.Jj, 11.10.Kk, 11.30.-j, 11.30.Na, 11.55.Fv, 03.65.Pm
The symmetry manifests itself in exact mathematical relations between the Bogoliubov coefficients for the processes induced by an accelerated point mirror in 1+1-dimensional space and the current (charge) densities for the processes caused by an accelerated point charge in 3+1-dimensional space. The spectra of pairs of Bose (Fermi) massless quanta emitted by the mirror coincide with the spectra of photons (scalar quanta) emitted by the electric (scalar) charge up to the factor 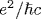 . The integral relation between the propagator of a pair of oppositely directed massless particles in 1+1-dimensional space and the propagator of a single particle in 3+1-dimensional space leads to the equality of the vacuum-vacuum amplitudes for the charge and the mirror if the mean number of created particles is small and the charge . The integral relation between the propagator of a pair of oppositely directed massless particles in 1+1-dimensional space and the propagator of a single particle in 3+1-dimensional space leads to the equality of the vacuum-vacuum amplitudes for the charge and the mirror if the mean number of created particles is small and the charge 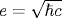 . Due to the symmetry, the mass shifts of electric and scalar charges (the sources of Bose fields with spin 1 and 0 in 3+1-dimensional space) for the trajectories with a subluminal relative velocity β12 of the ends and the maximum proper acceleration w0 are expressed in terms of the heat capacity (or energy) spectral densities of Bose and Fermi gases of massless particles with the temperature w0/2π in 1+1-dimensional space. Thus, the acceleration excites the 1-dimensional oscillations in the proper field of charges and the energy of oscillations is partly deexcited in the form of real quanta and partly remains in the field. As a result, the mass shift of an accelerated electric charge is nonzero and negative, while that of a scalar charge is zero. The symmetry is extended to the mirror and charge interactions with the fields carrying space-like momenta and defining the Bogoliubov coefficients αB,F. The traces . Due to the symmetry, the mass shifts of electric and scalar charges (the sources of Bose fields with spin 1 and 0 in 3+1-dimensional space) for the trajectories with a subluminal relative velocity β12 of the ends and the maximum proper acceleration w0 are expressed in terms of the heat capacity (or energy) spectral densities of Bose and Fermi gases of massless particles with the temperature w0/2π in 1+1-dimensional space. Thus, the acceleration excites the 1-dimensional oscillations in the proper field of charges and the energy of oscillations is partly deexcited in the form of real quanta and partly remains in the field. As a result, the mass shift of an accelerated electric charge is nonzero and negative, while that of a scalar charge is zero. The symmetry is extended to the mirror and charge interactions with the fields carrying space-like momenta and defining the Bogoliubov coefficients αB,F. The traces 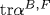 , which describe the vector and scalar interactions of the accelerated mirror with a uniformly moving detector, were found in analytic form for two mirror's trajectories with subluminal velocities of the ends. The symmetry predicts one and the same value , which describe the vector and scalar interactions of the accelerated mirror with a uniformly moving detector, were found in analytic form for two mirror's trajectories with subluminal velocities of the ends. The symmetry predicts one and the same value 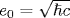 for the electric and scalar charges in 3+1-dimensional space. The arguments are adduced in favor of the conclusion that this value and the corresponding value α0=1/4π of the fine structure constant are the bare, nonrenormalized values. for the electric and scalar charges in 3+1-dimensional space. The arguments are adduced in favor of the conclusion that this value and the corresponding value α0=1/4π of the fine structure constant are the bare, nonrenormalized values.
|
|