BILAYER MEMBRANE IN CONFINED GEOMETRY: INTERLAYER SLIDE AND ENTROPIC REPULSION
Baoukina S.V., Mukhin S.I.

Received: April 28, 2004

PACS: 68.15.+e, 68.60.-Bs, 87.16.Dg

DJVU (172.3K)

PDF (362.3K)

We derive the free energy functional of a bilayer lipid membrane from the first principles of elasticity theory. The model explicitly includes position-dependent mutual slide of monolayers and bending deformation. Our free energy functional of a liquid-crystalline membrane allows for incompressibility of the membrane and vanishing of the in-plane shear modulus and obeys reflectional and rotational symmetries of the flat bilayer. Interlayer slide at the mid-plane of the membrane results in a local difference of the surface densities of monolayers. The slide amplitude directly enters the free energy via the strain tensor. For small bending deformations, the ratio between the bending modulus and the area compression coefficient, K_b/K_A, is proportional to the square of monolayer thickness h. Using the functional, we perform self-consistent calculation of the entropic potential acting on a bilayer between parallel confining walls separated by distance 2d. We find that at the minimum of the confining potential, the temperature-dependent curvature 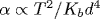is enhanced four times for a bilayer with slide as compared to a unit bilayer. We also calculate viscous modes of a bilayer membrane between confining walls. We investigate pure bending of the membrane, which is decoupled from area dilation at small amplitudes. Three sources of viscous dissipation are considered: water and membrane viscosities and interlayer drag. The dispersion relation gives two branches ω_1,2(q).