
ZhETF, Vol. 124,
No. 1,
p. 14 (July 2003)
(English translation - JETP,
Vol. 97, No. 1,
p. 10,
July 2003
available online at www.springer.com
)
THE SYMMETRY, INFERABLE FROM BOGOLIUBOV TRANSFORMATION, BETWEEN PROCESSES INDUCED BY A MIRROR IN 2-DIMENSIONAL AND A CHARGE IN 4-DIMENSIONAL SPACE-TIME
Ritus V.I.
Received: December 30, 2002
PACS: 11.10.Kk, 11.30.-j, 11.55.Fv, 03.65.Pm
We consider the symmetry between creation of pairs of massless bosons or fermions by an accelerated mirror in 1+1-dimensional space and emission of single photons or scalar quanta by an electric or scalar charge in 3+1-dimensional space. The relation of Bogoliubov coefficients describing the processes generated by the mirror to Fourier components of the current or charge density implies that the spin of any disturbances bilinear in the scalar or spinor field coincides with the spin of quanta emitted by the electric or scalar charge. The mass and invariant momentum transfer of these disturbances are essential for the relation of Bogoliubov coefficients to invariant singular solutions and the Green's functions of wave equations for both 1+1- and 3+1-dimensional spaces and especially for the integral relations between these solutions. One of these relations leads to the coincidence of the self-action changes and vacuum-vacuum amplitudes for an accelerated mirror in 2-dimensional space-time and a charge in 4-dimensional space-time. Both invariants of the Lorentz group, spin and mass, play an essential role in the established symmetry. The symmetry embraces not only the processes of real quanta radiation, but also the processes of the mirror and charge interactions with fields carring spacelike momenta. These fields accompany their sources and determine the Bogoliubov matrix coefficients αB,Fω'ω. It is shown that the Lorentz-invariant traces 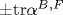 describe the vector and scalar interactions of the accelerated mirror with a uniformly moving detector. This interpretation rests essentially on the relation between propagators of the waves with spacelike momenta in 2- and 4-dimensional spaces. The traces describe the vector and scalar interactions of the accelerated mirror with a uniformly moving detector. This interpretation rests essentially on the relation between propagators of the waves with spacelike momenta in 2- and 4-dimensional spaces. The traces 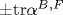 coincide with the products of the mass shift Δ m1,0 of the accelerated electric or scalar charge and the proper time of the shift formation. The symmetry fixes the value of the bare fine structure constant α0=1/4π. coincide with the products of the mass shift Δ m1,0 of the accelerated electric or scalar charge and the proper time of the shift formation. The symmetry fixes the value of the bare fine structure constant α0=1/4π.
|
|