PHYSICAL PROPERTIES OF SCALAR AND SPINOR FIELD STATES WITH THE RINDLER-MILNE (HYPERBOLIC) SYMMETRY
Ritus V.I.

Received: March 19, 2001

PACS: 11.10.-z, 11.30.-j

DJVU (114.1K)

PDF (265.2K)

It is shown that right and left combinations of the positive- and negative-frequency hyperbolically symmetric solutions of the Klein-Fock-Gordon equation possess an everywhere timelike current density vector with a definite Lorentz-invariant sign of the charge density, and similar combinations of solutions to the Dirac equation possess the energy-momentum tensor with everywhere real eigenvalues and a definite Lorentz-invariant sign of the energy density. These right and left modes, just as their 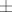-frequency components, are eigenfunctions of the Lorentz boost generator with the eigenvalue κ. The sign of the charge (energy) density coincides with the sign of κ for the right scalar (spinor) modes and is opposite to it for the left modes. It is then reasonable to assume that the particles (antiparticles) are precisely described by the right modes with κ >0 (κ <0) and by the left modes with κ <0 (κ >0).