VECTOR BOSON IN THE CONSTANT ELECTROMAGNETIC FIELD
Nikishov A.I.

Received: March 2, 2001

PACS: 03.65.Pm

DJVU (136.5K)

PDF (286.7K)

The propagator and the complete sets of in- and out-solutions of the wave equation, together with the Bogoliubov coefficients relating these solutions are obtained for the vector W boson (with the gyromagnetic ratio g=2) in the constant electromagnetic field. When only the electric field is present, the Bogoliubov coefficients are independent of the boson polarization and are the same as for the scalar boson. For the collinear electric and magnetic fields, the Bogoliubov coefficients for states with the boson spin perpendicular to the field are again the same as in the scalar case. For the W^- spin parallel (antiparallel) to the magnetic field, the Bogoliubov coefficients and the one-loop contributions to the imaginary part of the Lagrange function are obtained from the corresponding expressions for the scalar case by the substitution 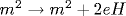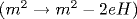. For the gyromagnetic ratio g=2, the vector boson interaction with the constant electromagnetic field is described by the functions that can be expected by comparing the scalar and Dirac particle wave functions in the constant electromagnetic field.