Journal of Experimental and Theoretical Physics

HOME | SEARCH | AUTHORS | HELP

Journal Issues

Manuscript Submission

Guidelines for Authors

Manuscript Status

Contacts

ZhETF, Vol. 120, No. 1, p. 5 (July 2001)
(English translation - JETP, Vol. 93, No. 1, p. 1, July 2001 available online at www.springer.com )

СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ ТЕОРИИ ВОЗМУЩЕНИЙ В ПРЕДЕЛЕ СИЛЬНОЙ СВЯЗИ. ФУНКЦИЯ ГЕЛЛ-МАННА-ЛОУ ТЕОРИИ \varphi⁴
Суслов И.М.

Received: December 27, 2000

PACS: 74.50.+r, 74.60.Ge, 74.25.Fy

DJVU (351.4K) PDF (898.8K)

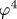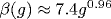Предложен алгоритм определения асимптотики суммы ряда теории возмущений в пределе сильной связи по заданным значениям его коэффициентов. Дана иллюстрация алгоритма на тестовых примерах, отработаны методика оценки ошибок и процедура оптимизации. Применение алгоритма к теории $\varphi^4$ дает для ее функции Гелл-Манна-Лоу поведение $\beta(g)\approx 7.4 g^{0.96}$ при больших g. 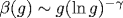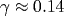Близость индекса к единице может быть интерпретирована как проявление логарифмического ветвления вида $\beta(g)\sim g (\ln g)^{-\gamma}$ с $\gamma\approx 0.14$ , в пользу чего есть независимые аргументы. 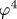В любом случае теория $\varphi^4$ является внутренне непротиворечивой. Обсуждается процедура суммирования рядов теории возмущений при произвольных значениях параметра разложения.

Report problems