
ZhETF, Vol. 119,
No. 1,
p. 45 (January 2001)
(English translation - JETP,
Vol. 92, No. 1,
p. 37,
January 2001
available online at www.springer.com
)
ОБОБЩЕННЫЕ ШТУРМОВСКИЕ РАЗЛОЖЕНИЯ КУЛОНОВСКОЙ ФУНКЦИИ ГРИНА И ДВУХФОТОННЫЕ ФОРМУЛЫ ГОРДОНА
Крыловецкий А.А., Манаков Н.Л., Мармо С.И.
Received: August 8, 2000
PACS: 32.80.-t, 32.10.Dk, 32.80.Rm
Радиальная часть кулоновской функции Грина (КФГ) записана в виде двойного ряда по полиномам Лагерра (функциям Штурма кулоновской задачи), содержащего два свободных параметра, α и α'. Результат применим как в нерелятивистском случае, так и для КФГ квадрированного уравнения Дирака с кулоновским потенциалом. При α = α' получено разложение КФГ на резонансную и потенциальную (гладко зависящую от энергии) части. В импульсном представлении КФГ со свободными параметрами записана в виде разложения по четырехмерным сферическим функциям. Выбор параметров α, α' в соответствии со спецификой конкретной задачи кардинально упрощает вычисление составных матричных элементов электромагнитных переходов. Получены замкнутые аналитические выражения (в записи через гипергеометрические функции) для амплитуд связанно-связанных и связанно-свободных двухфотонных переходов в атоме водорода из произвольного начального состояния \ket{nl}, обобщающие известные (однофотонные) формулы Гордона. Компоненты тензора динамической поляризуемости αnlm(ω) при произвольном n выражены через гипергеометрическую функцию 2F1, зависящую лишь от l и \tw, и полиномиальные функции fnl(\tw) частоты \tw =\hbarω/|En|. Исследованы ридберговская 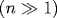 и припороговая и припороговая 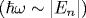 асимптотики поляризуемостей. асимптотики поляризуемостей.
|
|