A DIAGRAM TECHNIQUE FOR PERTURBATION THEORY CALCULATIONS OF THE EFFECTIVE CONDUCTIVITY OF TWO-DIMENSIONAL SYSTEMS
Khalatnikov I.M., Kamenshchik A.Yu.

Received: July 27, 2000

PACS: 03.50.De, 41.20.-q, 02.30.Nw, 72.80.Tm

The perturbation theory for calculating the effective conductivity of the plane consisting of pieces of different conductivities is constructed and a convenient diagram technique is elaborated for this perturbation theory. It is shown that for the chessboard, perturbative calculations give results that are in agreement with the well-known formula 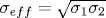. The components of the effective conductivity tensor for the anisotropic three-color chessboard are calculated. It is shown that the isotropic (symmetric) part of the effective conductivity calculated up to the sixth order of perturbation theory satisfies the Bruggeman effective medium equation for symmetric three-color structures with equally partitioned components. We also consider an isotropic three-color chessboard with nonequal weights of colors. In this case, the perturbation theory already in the fourth order contradicts the results following from the Bruggeman equation for nonequal weights.