О ГЕОМЕТРИИ ХАОТИЧЕСКОГО СЛОЯ
Шевченко И.И.

Received: March 13, 2000

PACS: 05.45.-a, 05.45.Pq, 45.20.Jj

Проводится анализ зависимости геометрической формы хаотического слоя в окрестности сепаратрисы нелинейного резонанса гамильтоновой системы от параметров последней. Рассматривается сепаратрисное алгоритмическое отображение, описывающее движение в окрестности сепаратрисы при наличии асимметричного возмущения с произвольной степенью асимметрии. Сепаратрисное алгоритмическое отображение представляет собой алгоритм, содержащий инструкции условного перехода. Выведена аналитическая процедура приведения сепаратрисного алгоритмического отображения к единой поверхности сечения исходной гамильтоновой системы (процедура синхронизации отображения). Обнаружено, что в случае высокочастотного возмущения 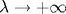(где λ - отношение частоты возмущения к частоте малых фазовых колебаний на резонансе) хаотический слой подвержен сильному изгибанию в том смысле, что при движении в окрестности сепаратрисы амплитуда отклонений по энергии относительно невозмущенного сепаратрисного значения много больше, чем ширина слоя. Однако синхронизированное сепаратрисное алгоритмическое отображение обеспечивает правильное представление фазового портрета слоя как при низких, так и при высоких значениях параметра λ, если амплитуда возмущения достаточно мала. Это продемонстрировано посредством сравнения фазовых портретов, полученных с помощью синхронизированного сепаратрисного алгоритмического отображения, с результатами прямого численного интегрирования исходной гамильтоновой системы.