РАССЕЯНИЕ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ НА ФОКУСИРОВАННОМ ЛАЗЕРНОМ ИМПУЛЬСЕ
Нарожный Н.Б., Фофанов М.С.

Received: November 26, 1999

PACS: Vk.41.75.-i

Решена задача о движении классического релятивистского электрона в фокусированном лазерном импульсе большой интенсивности. Для описания стационарного лазерного пучка предложена новая трехмерная модель электромагнитного поля, являющаяся точным решением уравнений Максвелла. Предложено обобщение модели, описывающее лазерный импульс конечной длительности и являющееся приближенным решением уравнений Максвелла. Выведены уравнения усредненного движения электрона в поле лазерного импульса, описываемого нашей моделью, в предположении слабых пространственной и временной неоднородностей поля. Показано, что в первом приближении по параметрам неоднородностей средняя (пондеромоторная) сила, действующая на частицу, определяется градиентом пондеромоторного потенциала, но теряет потенциальный характер уже во втором порядке. Обнаружена асимметричность трехмерного пондеромоторного потенциала. Получены траектории релятивистских электронов, движущихся в лазерном поле, и вычислены сечения рассеяния электронов на стационарном лазерном пучке. Показано, что в рассмотренной модели присутствуют эффект отражения электронов от лазерного импульса и серфинг-эффект. Оказалось, что асимметричный пондеромоторный потенциал при некоторых прицельных параметрах падающих электронов эффективно может проявлять себя как потенциал притяжения. Показано также, что сечение рассеяния даже в случае симметричного потенциала содержит сингулярности, известные под названием радужного рассеяния. Результаты применимы для полей, характеризующихся большими по сравнению с единицей значениями безразмерного параметра 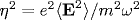и произвольных энергий электронов.