
ZhETF, Vol. 117,
No. 4,
p. 797 (April 2000)
(English translation - JETP,
Vol. 90, No. 4,
p. 695,
April 2000
available online at www.springer.com
)
СТАТИСТИЧЕСКИЙ ПРЕДЕЛ В ПОЛНОСТЬЮ ИНТЕГРИРУЕМОЙ СИСТЕМЕ ПРИ ДЕТЕРМИНИРОВАННЫХ НАЧАЛЬНЫХ УСЛОВИЯХ
Гуревич А.В., Мазур Н.Г., Зыбин К.П.
Received: October 5, 1999
PACS: 05.10.-a, 05.45.Yv
Исследуется асимптотическое поведение решений уравнения КдВ в квазиклассическом пределе при заданной на всей оси x осциллирующей непериодической начальной функции u0(x). При таком начальном условии в системе развиваются нелинейные колебания, которые в асимптотике 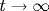 приобретают стохастический характер. Сформулирована полная система законов сохранения в интегральной форме и продемонстрирована ее эквивалентность спектральной плотности дискретных уровней начальной задачи. Рассмотрена задача рассеяния для уравнения Шредингера с начальным потенциалом -u0(x) и показано, что фаза рассеяния является равномерно распределенной случайной величиной. Разработан модифицированный метод решения обратной задачи рассеяния путем построения максимизатора для N-солитонного решения со случайными начальными фазами. Установлена взаимно однозначная связь между спектром дискретных уровней начального состояния системы и установившимся спектром в пространстве фаз. Показано, что при переходе системы в стохастическое состояние выполняются все интегральные законы сохранения КдВ, причем первые три точно, а остальные в приближении ВКБ, т. е. с точностью до квадрата малого дисперсионного параметра. Введено понятие квазисолитона, играющего в стохастическом состоянии системы роль обычного солитона в динамическом пределе. Развит метод определения плотности вероятности f(u), и проведен ее расчет для конкретной начальной проблемы. Физически рассмотренная задача описывает развитое состояние одномерной турбулентности в дисперсионной гидродинамике. приобретают стохастический характер. Сформулирована полная система законов сохранения в интегральной форме и продемонстрирована ее эквивалентность спектральной плотности дискретных уровней начальной задачи. Рассмотрена задача рассеяния для уравнения Шредингера с начальным потенциалом -u0(x) и показано, что фаза рассеяния является равномерно распределенной случайной величиной. Разработан модифицированный метод решения обратной задачи рассеяния путем построения максимизатора для N-солитонного решения со случайными начальными фазами. Установлена взаимно однозначная связь между спектром дискретных уровней начального состояния системы и установившимся спектром в пространстве фаз. Показано, что при переходе системы в стохастическое состояние выполняются все интегральные законы сохранения КдВ, причем первые три точно, а остальные в приближении ВКБ, т. е. с точностью до квадрата малого дисперсионного параметра. Введено понятие квазисолитона, играющего в стохастическом состоянии системы роль обычного солитона в динамическом пределе. Развит метод определения плотности вероятности f(u), и проведен ее расчет для конкретной начальной проблемы. Физически рассмотренная задача описывает развитое состояние одномерной турбулентности в дисперсионной гидродинамике.
|
|