ПОГЛОЩЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ЭНЕРГИИ МЕДЛЕННЫМ ЭЛЕКТРОНОМ ПРИ РАССЕЯНИИ НА КУЛОНОВСКОМ ЦЕНТРЕ
Крайнов В.П.

Поступила в редакцию: 3 Января 2001

PACS: 36.40.-c, 52.40.Nk, 61.46.+w

DJVU (94K)

PDF (259.9K)

Получены простые аналитические выражения для вероятности вынужденного обратного тормозного поглощения в единицу времени при рассеянии электрона на кулоновском центре с зарядом Z в присутствии электромагнитного поля. Начальная и конечная энергия электрона предполагаются малыми по сравнению с ридберговской энергией Z² (всюду используются атомные единицы). Рассматриваются однофотонные процессы поглощения и вынужденного излучения фотона электроном. Предполагается, что частота электромагнитного поля ω достаточно мала, так что выполняется условие 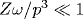, где p - импульс электрона, а также условие . 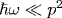Однако эта частота предполагается достаточно большой по сравнению с частотой столкновения электрона с кулоновскими центрами: . Получены зависимости вероятностей поглощения и вынужденного излучения фотона от угла θ между направлением падающего электрона и вектором поляризации электромагнитного поля (предполагаемого линейно поляризованным). Показано, что при любых углах θ вероятность поглощения фотона больше вероятности вынужденного излучения, и, таким образом, эффект Маркуза для медленных электронов (усиление электромагнитного поля) отсутствует. Показано также, что медленный электрон в среднем поглощает удвоенную пондеромоторную энергию за одно столкновение с ионом (кулоновским центром) в максвелловской плазме. Это совпадает как с известными результатами расчетов для быстрых электронов, так и с известными результатами расчета, исходящего из классического кинетического уравнения Больцмана для плазмы.