
ЖЭТФ, Том 156,
Вып. 2,
стр. 348 (Август 2019)
(Английский перевод - JETP,
Vol. 129, No 2,
August 2019
доступен on-line на www.springer.com
)
Осцилляции Шубникова-де Гааза термоэлектрического поля в слоистых проводниках вблизи топологического перехода Лифшица
Песчанский В.Г., Галбова О., Ясемидис К.
Поступила в редакцию: 23 Января 2019
DOI: 10.1134/S0044451019080133
Исследован отклик на неоднородный разогрев слоистого проводника с квазидвумерным электронным энергетическим спектром с многолистной поверхностью Ферми (ПФ), состоящей из слабогофрированных цилиндров и примыкающих к ним двух планарных листов. В результате воздействия на проводник давления либо допирования примесными атомами можно настолько уменьшить расстояние Δ p между цилиндром и планарными листами ПФ, что электроны проводимости начнут блуждать по ним, туннелируя с одного листа (полости) ПФ на другой. Если за время свободного пробега электрон проводимости успевает несколько раз посетить все листы ПФ, то его движение в плоскости, ортогональной магнитному полю, становится финитным. При этом возникают осцилляции Шубникова-де Гааза, период которых определяется замкнутой площадью, описываемой электроном при своем движении по магнитопробойной траектории в импульсном пространстве. Рассчитана зависимость термоэлектрического поля от величины и ориентации достаточно сильного квантующего магнитного поля. В магнитном поле, нормальном к слоям, сечения цилиндрической части ПФ равноудалены от обоих планарных листов ПФ. Однако даже при небольшом отклонении поля от нормали к слоям на угол 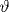 эта равноудаленность нарушается, и при некоторых значениях угла эта равноудаленность нарушается, и при некоторых значениях угла 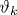 вероятность магнитного пробоя на один из планарных листов ПФ может быть настолько мала, что электрон не может замкнуть магнитопробойную траекторию, а его движение по другому планарному листу с посещением цилиндрической части ПФ становится инфинитным. При этом магнитопробойные квантовые осцилляции намагниченности и всех кинетических характеристик проводника исчезают, а их исчезновение периодически повторяется с изменением угла наклона магнитного поля к слоям как функция \tg \vartheta . вероятность магнитного пробоя на один из планарных листов ПФ может быть настолько мала, что электрон не может замкнуть магнитопробойную траекторию, а его движение по другому планарному листу с посещением цилиндрической части ПФ становится инфинитным. При этом магнитопробойные квантовые осцилляции намагниченности и всех кинетических характеристик проводника исчезают, а их исчезновение периодически повторяется с изменением угла наклона магнитного поля к слоям как функция \tg \vartheta .
|
|