
ЖЭТФ, Том 146,
Вып. 2,
стр. 373 (Август 2014)
(Английский перевод - JETP,
Vol. 119, No 2,
p. 331,
August 2014
доступен on-line на www.springer.com
)
УСТРАНЕНИЕ ПАРАДОКСА ЛИНЕЙНОЙ УСТОЙЧИВОСТИ ТЕЧЕНИЯ ХАГЕНА - ПУАЗЕЙЛЯ И ВЯЗКИЙ ДИССИПАТИВНЫЙ МЕХАНИЗМ ВОЗНИКНОВЕНИЯ ТУРБУЛЕНТНОСТИ В ПОГРАНИЧНОМ СЛОЕ
Чефранов С.Г., Чефранов А.Г.
Поступила в редакцию: 13 Декабря 2013
DOI: 10.7868/S0044451014080148
Показано, что для получения вывода о линейной неустойчивости течения Хагена - Пуазейля при конечных числах Рейнольдса необходимо отказаться от использования традиционной «нормальной» формы представления возмущений, которая предполагает возможность разделения переменных, описывающих изменчивость возмущений в зависимости от радиальной и продольной (вдоль оси трубы) координат. При отсутствии такого разделения переменных в развиваемой линейной теории предложено использовать такую модификацию метода Бубнова - Галеркина, которая дает возможность учета различия периодов продольной изменчивости для разных радиальных мод, определяемых предварительно в результате стандартного применения метода Галеркина - Канторовича к уравнению эволюции предельно малых аксиально-симметричных возмущений тангенциальной компоненты поля скорости. Установлено, что при рассмотрении даже двух линейно взаимодействующих радиальных мод для течения Хагена - Пуазейля линейная неустойчивость возможна лишь при наличии указанной условно периодической продольной изменчивости возмущений вдоль оси трубы, когда пороговое значение числа Рейнольдса 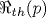 очень чувствительно зависит от отношения p двух продольных периодов, каждый из которых описывает продольную изменчивость только для своей радиальной моды возмущений. При этом очень чувствительно зависит от отношения p двух продольных периодов, каждый из которых описывает продольную изменчивость только для своей радиальной моды возмущений. При этом 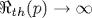 лишь для случаев, когда величина p принимает любое из следующих значений: p=pk=k, p\qqq=p1/k\qqq=1/k, p\qqq=p\sqrt{k} \qqq=\left[k+1\pm\sqrt{(k+1)2-4} \right]/2, где лишь для случаев, когда величина p принимает любое из следующих значений: p=pk=k, p\qqq=p1/k\qqq=1/k, p\qqq=p\sqrt{k} \qqq=\left[k+1\pm\sqrt{(k+1)2-4} \right]/2, где 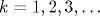 Полученное для реализации линейной неустойчивости течения Хагена - Пуазейля минимальное число Полученное для реализации линейной неустойчивости течения Хагена - Пуазейля минимальное число 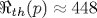 (когда (когда 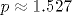 ) количественно соответствует условию возбуждения волн Толмина - Шлихтинга в пограничном слое, где также ) количественно соответствует условию возбуждения волн Толмина - Шлихтинга в пограничном слое, где также 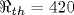 . Рассматривается сходство механизмов линейной вязкой диссипативной неустойчивости для течения Хагена - Пуазейля и волн Толмина - Шлихтинга. Получено хорошее количественное соответствие величин фазовых скоростей рассматриваемых вихревых возмущений с данными экспериментов о скоростях переднего и заднего фронтов турбулентных «пробок», распространяющихся вдоль оси трубы. . Рассматривается сходство механизмов линейной вязкой диссипативной неустойчивости для течения Хагена - Пуазейля и волн Толмина - Шлихтинга. Получено хорошее количественное соответствие величин фазовых скоростей рассматриваемых вихревых возмущений с данными экспериментов о скоростях переднего и заднего фронтов турбулентных «пробок», распространяющихся вдоль оси трубы.
|
|