
|
 |

ЖЭТФ, Том 141,
Вып. 5,
стр. 983 (Май 2012)
(Английский перевод - JETP,
Vol. 114, No 5,
p. 857,
May 2012
доступен on-line на www.springer.com
)
ПОПЕРЕЧНАЯ НЕУСТОЙЧИВОСТЬ ПЛОСКОГО ФРОНТА БЫСТРЫХ ВОЛН УДАРНОЙ ИОНИЗАЦИИ
Кюрегян А.С.
Поступила в редакцию: 25 Июля 2011
Проведен теоретический анализ поперечной неустойчивости плоского фронта быстрых волн ударной ионизации (ВУИ) в полупроводниковых структурах p+-n-n+ с конечной концентрацией N доноров в n-слое. Предполагалось, что высокая скорость u ВУИ обеспечивается за счет лавинного размножения однородного фона электронов и дырок, концентрация σb которых перед фронтом достаточно велика для применимости континуального приближения. Проблема вычисления инкремента s нарастания малого гармонического возмущения с волновым числом k сведена к задаче на собственные значения своеобразного однородного уравнения типа Вольтерра второго рода, содержащего сумму двукратных и трехкратного интегралов от неизвестной собственной функции. Эта задача решалась методом последовательных приближений. Показано, что при малых k функция s(k) монотонно возрастает в соответствии с аналитической теорией [12], достигает максимума sM при k=kM, после чего уменьшается и становится отрицательной при k>k01. Такой характер зависимости s(k) коротковолновых возмущений обусловлен ослаблением искажения поля из-за конечной толщины области пространственного заряда фронта и «размазыванием» возмущения концентраций за счет поперечного переноса носителей заряда. Установлены законы подобия для возмущений с 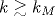 : при фиксированных значениях σb и максимальной напряженности поля на фронте E0M инкремент s зависит только от отношения k/N, а граничное волновое число : при фиксированных значениях σb и максимальной напряженности поля на фронте E0M инкремент s зависит только от отношения k/N, а граничное волновое число 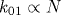 . Приведены зависимости от E0M параметров sM, kM и k01, определяющих динамику нарастания возмущений и верхнюю границу области неустойчивости ВУИ. Эти зависимости указывают на то, что модель плоской ВУИ оказывается недостаточной для описания работы лавинных обострителей напряжения и что в рамках континуального приближения фронты быстрых стримеров должны быть устойчивыми по отношению к поперечным возмущениям в соответствии с опубликованными ранее результатами численного моделирования. Полученные результаты подтверждены путем численного моделирования эволюции малых гармонических возмущений плоской стационарной ВУИ. . Приведены зависимости от E0M параметров sM, kM и k01, определяющих динамику нарастания возмущений и верхнюю границу области неустойчивости ВУИ. Эти зависимости указывают на то, что модель плоской ВУИ оказывается недостаточной для описания работы лавинных обострителей напряжения и что в рамках континуального приближения фронты быстрых стримеров должны быть устойчивыми по отношению к поперечным возмущениям в соответствии с опубликованными ранее результатами численного моделирования. Полученные результаты подтверждены путем численного моделирования эволюции малых гармонических возмущений плоской стационарной ВУИ.
|
|
|