
ЖЭТФ, Том 141,
Вып. 1,
стр. 135 (Январь 2012)
(Английский перевод - JETP,
Vol. 114, No 1,
p. 118,
January 2012
доступен on-line на www.springer.com
)
ВЛИЯНИЕ ДЫРОЧНОГО ДОПИРОВАНИЯ НА ЭЛЕКТРОННУЮ СТРУКТУРУ И ПОВЕРХНОСТЬ ФЕРМИ В МОДЕЛИ ХАББАРДА В РАМКАХ КЛАСТЕРНОЙ ТЕОРИИ ВОЗМУЩЕНИЙ С КОНТРОЛИРУЕМЫМ СПЕКТРАЛЬНЫМ ВЕСОМ
Николаев С.В., Овчинников С.Г.
Поступила в редакцию: 3 Марта 2011
Исследованы концентрационные зависимости зонной структуры, спектрального веса, плотности состояний и поверхности Ферми в парамагнитном состоянии модели Хаббарда в теории возмущений с 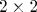 -кластерами. Представление X-операторов Хаббарда позволяет контролировать сохранение спектрального веса при построении теории возмущений. Вычисленная энергия основного состояния находится в хорошем согласии с такими непертурбативными методами, как квантовый метод Монте-Карло, точная диагонализация -кластерами. Представление X-операторов Хаббарда позволяет контролировать сохранение спектрального веса при построении теории возмущений. Вычисленная энергия основного состояния находится в хорошем согласии с такими непертурбативными методами, как квантовый метод Монте-Карло, точная диагонализация 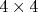 -кластера и вариационный метод Монте-Карло. Показано, что внутрищелевые состояния при дырочном допировании расположены вблизи потолка нижней зоны Хаббарда при больших U и вблизи дна верхней зоны при малых U. Концентрационная зависимость поверхности Ферми сильно зависит от перескоков на вторые (t') и третьи (t'') соседи. При характерных для ВТСП-купратов значениях параметров показано существование трех концентрационных областей с разными поверхностями Ферми. Показано, что уширение спектральной плотности электронов с типичным для современного ARPES энергетическим разрешением приводит к картинке арок с длиной, зависящей от концентрации. Только уменьшение ширины линии на порядок позволит получить из спектральной плотности истинную поверхность Ферми. В законе дисперсии ниже уровня Ферми обнаружены кинки, обусловленные сильными электронными корреляциями. -кластера и вариационный метод Монте-Карло. Показано, что внутрищелевые состояния при дырочном допировании расположены вблизи потолка нижней зоны Хаббарда при больших U и вблизи дна верхней зоны при малых U. Концентрационная зависимость поверхности Ферми сильно зависит от перескоков на вторые (t') и третьи (t'') соседи. При характерных для ВТСП-купратов значениях параметров показано существование трех концентрационных областей с разными поверхностями Ферми. Показано, что уширение спектральной плотности электронов с типичным для современного ARPES энергетическим разрешением приводит к картинке арок с длиной, зависящей от концентрации. Только уменьшение ширины линии на порядок позволит получить из спектральной плотности истинную поверхность Ферми. В законе дисперсии ниже уровня Ферми обнаружены кинки, обусловленные сильными электронными корреляциями.
|
|