ДЕТЕРМИНИСТИЧЕСКИЕ МЕТОДИКИ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ ЛАВИН УБЕГАЮЩИХ ЭЛЕКТРОНОВ ВЫСОКИХ ЭНЕРГИЙ
Бабич Л.П., Бочков Е.И.

Поступила в редакцию: 23 Июня 2010

DJVU (146.7K)

PDF (339.4K)

Анализируются возможности двух детерминистических методик описания кинетики убегающих электронов (УЭ) высоких энергий как альтернативные стохастическим методикам, требующим нереально больших вычислительных ресурсов в задачах численного моделирования электрических разрядов в плотных газах с участием УЭ. Одна из методик, развиваемая в последние годы, основана на многогрупповых уравнениях для моментов функции распределения электронов, вторая, традиционная для решения задач газового разряда, - на уравнении переноса в диффузионно-дрейфовом приближении. Методика многогрупповых уравнений в современном состоянии позволяет вычислять распределение УЭ по энергиям и пространственное распределение вдоль электрической силы, которые при соответствующем числе энергетических групп N близки к распределениям, полученным методом Монте-Карло. Диффузионно-дрейфовое уравнение не дает распределения по энергиям, но его достоинством является возможность получать с малыми затратами вычислительных ресурсов распределения УЭ в пространстве не только вдоль, но и поперек электрической силы, близкие к результатам расчетов методом Монте-Карло. Для моделирования разрядов методом многогрупповых уравнений необходимо априорное знание числа групп N, обеспечивающего хорошую точность, характерного времени размножения УЭ t_e и энергетического порога убегания 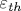как функций перенапряжения электрического поля. В методике диффузионно-дрейфового уравнения, кроме t_e, необходимо задавать направленную скорость УЭ и коэффициенты продольной и поперечной диффузии, вычисляемые методом Монте-Карло.