
ЖЭТФ, Том 138,
Вып. 4,
стр. 595 (Октябрь 2010)
(Английский перевод - JETP,
Vol. 111, No 4,
p. 525,
October 2010
доступен on-line на www.springer.com
)
ФЛУКТУАЦИИ ЭНТРОПИИ ЗАПУТАННОСТИ В КВАНТОВЫХ ЦЕПОЧКАХ ИЗИНГА
Юрищев М.А.
Поступила в редакцию: 25 Февраля 2010
Рассматриваются цепочки Изинга в поперечном магнитном поле постоянной напряженности (h=1) и величиной межспиновых взаимодействий λ. В случае бесконечно длинной цепочки найдены точные аналитические формулы для второго центрального момента (дисперсии) оператора энтропии 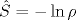 с редуцированной матрицей плотности ρ, которая соответствует полубесконечной части модели, находящейся в основном состоянии. Показано, что в окрестности критической точки λc=1 флуктуация энтропии запутанности Δ S (квадратный корень из дисперсии) расходится по закону с редуцированной матрицей плотности ρ, которая соответствует полубесконечной части модели, находящейся в основном состоянии. Показано, что в окрестности критической точки λc=1 флуктуация энтропии запутанности Δ S (квадратный корень из дисперсии) расходится по закону ![\Delta S\sim[\ln(1/|1-\lambda|)]^{1/2}](/img/latex/x5cDeltax20Sx5csimx5bx5clnx281x2fx7c1x2dx5clambdax7cx29x5dx5ex7b1x2f2x7d.png) . С учетом известного поведения самой запутанности S это приводит к тому, что в критической точке величина относительных флуктуаций энтропии запутанности δ S=Δ S/S обращается в нуль, т. е. реализуется состояние, фактически, с нефлуктуирующей запутанностью. . С учетом известного поведения самой запутанности S это приводит к тому, что в критической точке величина относительных флуктуаций энтропии запутанности δ S=Δ S/S обращается в нуль, т. е. реализуется состояние, фактически, с нефлуктуирующей запутанностью.
|
|