
ЖЭТФ, Том 138,
Вып. 3,
стр. 508 (Сентябрь 2010)
(Английский перевод - JETP,
Vol. 111, No 3,
p. 450,
September 2010
доступен on-line на www.springer.com
)
АСИМПТОТИКА β-ФУНКЦИИ В ТЕОРИИ \varphi4: СХЕМА БЕЗ КОМПЛЕКСНЫХ ПАРАМЕТРОВ
Суслов И.М.
Поступила в редакцию: 3 Марта 2010
Полученные ранее аналитические асимптотики при g→∞ для функции Гелл-Манна - Лоу β(g) и аномальных размерностей в теории 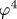 основаны на параметрическом представлении типа g=f(t), β(g)=f1(t) (где основаны на параметрическом представлении типа g=f(t), β(g)=f1(t) (где 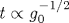 - бегущий параметр, связанный с затравочным зарядом g0), которое упрощается в комплексной плоскости t вблизи нуля одного из функциональных интегралов. Ниже показано, что параметрическое представление имеет сингулярность при t→ 0, что позволяет получить аналогичные результаты при действительных значениях g0. Одновременно решается вопрос о правильном характере предельного перехода к режиму сильной связи; в частности, постоянство затравочной или перенормированной массы не является правильным условием предельного перехода. Дано частичное доказательство «теоремы о перенормируемости» для области сильной связи. - бегущий параметр, связанный с затравочным зарядом g0), которое упрощается в комплексной плоскости t вблизи нуля одного из функциональных интегралов. Ниже показано, что параметрическое представление имеет сингулярность при t→ 0, что позволяет получить аналогичные результаты при действительных значениях g0. Одновременно решается вопрос о правильном характере предельного перехода к режиму сильной связи; в частности, постоянство затравочной или перенормированной массы не является правильным условием предельного перехода. Дано частичное доказательство «теоремы о перенормируемости» для области сильной связи.
|
|